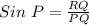Answer:
The correct option is option (c).
Explanation:
Right angled triangle:
- One angle must be 90° and other two angles are acute angle.
- The hypotenuses is the longest side of the triangle and opposite right angle.
- It follows the Pythagorean Theorem.
Given that,
∠QRP= 90°, ∠RPQ= 30°, ∠PQR = 60°
we know that,
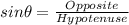
for sin P , the opposite is QR.
The hypotenuse is PQ.
Therefore,