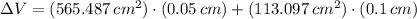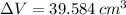Question

Use differentials to estimate the amount of material in a closed cylindrical can that is 30 cm high and 12 cm in diameter if the metal in the top and bottom is 0.1 cm thick, and the metal in the sides is 0.05 cm thick. Note, you are approximating the volume of metal which makes up the can (i.e. melt the can into a blob and measure its volume), not the volume it encloses.

Answer 1

`\Delta V = 39.584\,cm^(3)`

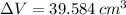
Explanation:

The volume of the diameter is:

`V = (\pi)/(4)\cdot D^(2)\cdot l`

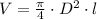
The differential of this expression is:

`\Delta V = (\partial V)/(\partial D) \cdot \Delta D + (\partial V)/(\partial L) \cdot \Delta L`

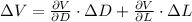
The partial derivatives are presented hereafter:

`(\partial V)/(\partial D) = (\pi)/(2)\cdot D\cdot l`

`(\partial V)/(\partial D) = (\pi)/(2)\cdot (12\,cm)\cdot (30\,cm)`

`(\partial V)/(\partial D) \approx 565.487\,cm^(2)`

`(\partial V)/(\partial l) = (\pi)/(4)\cdot D^(2)`

`(\partial V)/(\partial l) = (\pi)/(4)\cdot (12\,cm)^(2)`

`(\partial V)/(\partial l) \approx 113.097\,cm^(2)`

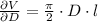
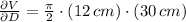
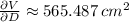
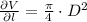
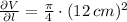
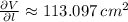
The thickness in the sides is related to the diameter, whereas the thickness in the top and bottom is related to the height. The estimated amount of material is:

`\Delta V = (565.487\,cm^(2))\cdot (0.05\,cm) + (113.097\,cm^(2))\cdot (0.1\,cm)`

`\Delta V = 39.584\,cm^(3)`