Question

F(x) = -4x^2+10x-8f(x)=−4x 2 +10x−8f, left parenthesis, x, right parenthesis, equals, minus, 4, x, squared, plus, 10, x, minus, 8 What is the value of the discriminant of fff? How many distinct real number zeros does fff have?

Answer 1

The value of Discriminant is -28.

The discriminant is negative, it implies that the function has no real solution.

Explanation:

Given,

`f(x)=-4x^2+10x-8`

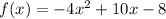
We need to find the value of discriminant.

And also we need to find the number of real zeros 'f(x)' have.

Solution,

We have given the quadratic equation;

`f(x)=-4x^2+10x-8`

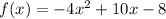
where

`a = -4\\\\b = 10\\\\c = -8`

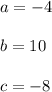
Now we will find the Discriminant.

Discriminant can be calculated by using the formula
`b^2 - 4ac`.

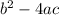Substituting the values we get;

`D=b^2 - 4ac = 10^2-4*(-4)*(-8)=100-128 =-28`

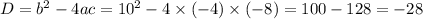
Hence the value of Discriminant is -28.

Since the discriminant is negative, it implies that the function has no real solution.