Question

To measure the height of a tree, a surveyor walked a short distance from the tree and found the angle of elevation was 43.9°, then walked 20 feet farther and measured the angle of elevation to be 37.6°. Find the height of the tree.

Answer 1

The height of the tree is H = 77.06 m

Explanation:

From Δ ABC

AB = height of the tree

`\tan 43.9 = (AB)/(BC)`

`\tan 43.9 = (h)/(x)`

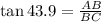
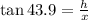
h = 0.9623 x ------- (1)

From Δ ABD

`\tan 37.6 = (h)/(20+ x)`

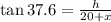
h = 0.77 (x + 20) ----- (2)

Equating Equation 1 & 2 we get

0.9623 x = 0.77 (x + 20)

0.9623 x = 0.77 x + 15.4

x (0.1923) = 15.4

x = 80.08 m

Thus the height of the tree is given by

H = 0.9623 x

H = 0.9623 × 80.08

H = 77.06 m

Therefore the height of the tree is H = 77.06 m