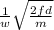Answer:
Step-by-step explanation:
Let mass of the apparatus be m .
applying work-energy theorem
work done = kinetic energy
f x d = 1/2 m v² , v is velocity acquired by apparatus
v =

The apparatus will start moving on a circular path with radius of w ( additional length of string )
radius of circle = w
velocity on the circular path = v
angular velocity = linear velocity / radius
= v / w
=