Question

6.01 Properties of Exponents

Practice
Active
2
Explain why rational exponents are not defined when the denominator of the exponent in lowest terms is even and the base is
negative.​

Answer 1

Rational exponents are not defined when the denominator of the exponent in lowest terms is even and the base is negative.

Explanation:

Considering the expression

`X^{(a)/(b)}=\sqrt[b]{X^a};\:\:\:\:\:\:\:\:\:b\\e 0`

Here:

• b = index

• a = exponent

• X = radicand

• √ = radical symbol

A rational exponent - an exponent that is a fraction - is the kind of way we may write a root.

If the denominator is an even number, it means we are talking about an even root like square root, 4th root, 6th root etc.

For example, think about squaring a number

-4 × -4 = 16, 4 × 4 = 16

It means any number when it get multiplied by itself an even number of times, it would always yield a positive number.

It is not possible to take the square root of a negative number as we can not yield a negative number when we square the number. In other words, there is no way we can multiply the same negative number twice and get a negative number. This is why
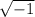`√(-1)` is undefined.

Therefore, rational exponents are not defined when the denominator of the exponent in lowest terms is even and the base is negative.