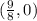Question

Find the critical points of the function f(x, y) = 8y2x − 8yx2 + 9xy. Determine whether they are local minima, local maxima, or saddle points. (Order your answers from smallest to largest x, then from smallest to largest y.)

Answer 1

Saddle point:
`(0,0)`

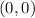
Local minimum:
`((3)/(8), -(3)/(8))`

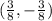
Local maxima:
`(0,-(9)/(8))`,
`((9)/(8),0)`

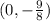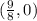
Explanation:

The function is:

`f(x,y) = 8\cdot y^(2)\cdot x -8\cdot y\cdot x^(2) + 9\cdot x \cdot y`

The partial derivatives of the function are included below:

`(\partial f)/(\partial x) = 8\cdot y^(2)-16\cdot y\cdot x+9\cdot y`

`(\partial f)/(\partial x) = y \cdot (8\cdot y -16\cdot x + 9)`

`(\partial f)/(\partial y) = 16\cdot y \cdot x - 8 \cdot x^(2) + 9\cdot x`

`(\partial f)/(\partial y) = x \cdot (16\cdot y - 8\cdot x + 9)`

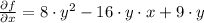
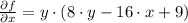
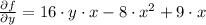
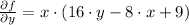
Local minima, local maxima and saddle points are determined by equalizing both partial derivatives to zero.

`y \cdot (8\cdot y -16\cdot x + 9) = 0`

`x \cdot (16\cdot y - 8\cdot x + 9) = 0`

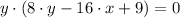
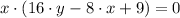
It is quite evident that one point is (0,0). Another point is found by solving the following system of linear equations:

`\left \{ {{-16\cdot x + 8\cdot y=-9} \atop {-8\cdot x + 16\cdot y=-9}} \right.`

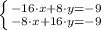
The solution of the system is (3/8, -3/8).

Let assume that y = 0, the nonlinear system is reduced to a sole expression:

`x\cdot (-8\cdot x + 9) = 0`

Another solution is (9/8,0).

Now, let consider that x = 0, the nonlinear system is now reduced to this:

`y\cdot (8\cdot y+9) = 0`

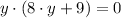
Another solution is (0, -9/8).

The next step is to determine whether point is a local maximum, a local minimum or a saddle point. The second derivative test:

`H = (\partial^(2) f)/(\partial x^(2)) \cdot (\partial^(2) f)/(\partial y^(2)) - (\partial^(2) f)/(\partial x \partial y)`

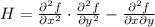
The second derivatives of the function are:

`(\partial^(2) f)/(\partial x^(2)) = 0`

`(\partial^(2) f)/(\partial y^(2)) = 0`

`(\partial^(2) f)/(\partial x \partial y) = 16\cdot y -16\cdot x + 9`

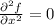
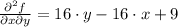
Then, the expression is simplified to this and each point is tested:

`H = -16\cdot y +16\cdot x -9`

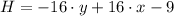
S1: (0,0)

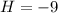`H = -9` (Saddle Point)

S2: (3/8,-3/8)

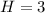`H = 3` (Local maximum or minimum)

S3: (9/8, 0)

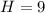`H = 9` (Local maximum or minimum)

S4: (0, - 9/8)

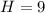`H = 9` (Local maximum or minimum)

Unfortunately, the second derivative test associated with the function does offer an effective method to distinguish between local maximum and local minimums. A more direct approach is used to make a fair classification:

S2: (3/8,-3/8)

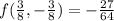`f((3)/(8) ,-(3)/(8) ) = - (27)/(64)` (Local minimum)

S3: (9/8, 0)

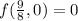`f((9)/(8),0) = 0` (Local maximum)

S4: (0, - 9/8)

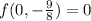`f(0,-(9)/(8) ) = 0` (Local maximum)

Saddle point:
`(0,0)`

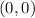
Local minimum:
`((3)/(8), -(3)/(8))`

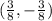
Local maxima:
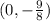`(0,-(9)/(8))`,
`((9)/(8),0)`