Question

What is the molality of a solution of 1.25 moles of sugar dissolved in 0.750 kg of water? What is the boiling point and freezing point of the resulting solutions?

Answer 1

1.67 m is the molality of a solution .

The boiling point of a solution is 100.85°C.

The freezing point of a solution is -3.1°C.

Step-by-step explanation:

`Molality=\frac{\text{Moles of solute}}{\text{mass of solvent in kg}}`

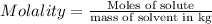
Moles of sugar = 1.25 mol

Mass of water = 0.750 kg

Molality of the solution ;

`m=(1.25 mol)/(0.750 kg)=1.67 m`

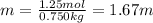
1.67 m is the molality of a solution .

Freezing point of the resulting solution

`\Delta T_b=T_b-T'`

`\Delta T_b=K_b* m`

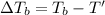
where,

`\Delta T_b` =elevation in boiling point =

T' = Boiling point of pure solvent

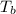`T_b` = boiling point of solution

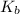`K_b` = boiling point constant

m = molality

we have :

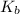`K_b` of water = 0.512 °C/m ,

m = 1.67 m

`\Delta T_b=0.512^oC* 1.67 m`

`\Delta T_b=0.85^oC`

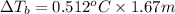
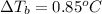
Boiling point of pure water = T' = 100°C

Boiling point of solution =
`T_b`

`T_b=T'+\Delta T_b=100^oC+0.85^oC=100.85^oC`

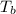
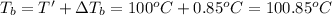
The boiling point of a solution is 100.85°C.

Freezing point of the resulting solution

`\Delta T_f=T-T_f`

`\Delta T_f=K_f* m`

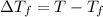
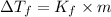
where,

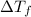`\Delta T_f` =depression in freezing point =

T = Freezing point of pure solvent

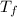`T_f` = Freezing point of solution

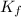`K_f` = freezing point constant

m = molality

we have :

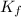`K_f` of water = 1.86°C/m ,

m = 1.67 m

`\Delta T_f=1.86^oC* 1.67 m`

`\Delta T_f=3.1^oC`

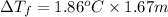
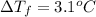
Freezing point of pure water = T = 0°C

Freezing point of solution =
`T_f`

`T_f=T-\Delta T_f=0^oC-3.1^oC=-3.1^oC`

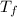
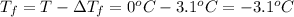
The freezing point of a solution is -3.1°C.