Answer:
4 times larger (circumference)
Explanation:
Basically the question is asking:
If radius of a circle becomes 4 times larger, how many times larger is the circumference of the circle?
Let take the original picture radius as "r", so the circumference would be:

Now, if the radius is 4 times larger, the new radius is "4r", so the circumference would be:
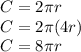
The number of times it is larger is found by taking the new circumference by original circumference, shown below:
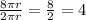
So, the circumference appears 4 times larger