Question

Lucas and Erick are factoring the polynomial 12x ^ 3 - 6x ^ 2 + 8x - 4 4. Lucas groups the polynomial (12x^ 3 + 8x)+(-6x^ 2 -4) to factor Erick groups the polynomial (12x ^ 3 - 6x ^ 2) + (8x - 4) to factor Who correctly grouped the terms to factor ? Explain .

Answer 1

sample response:Both students are correct because polynomials can be grouped in different ways to factor. Both ways result in a common binomial factor between the groups. Using the distributive property , this common binomial term can be factored out. Each grouping results in the same two binomial factors.

Answer 2

Both factor can correctly grouped the terms to factor.

Explanation:

Given two polynomial,

`12x^3-6x^2+8x-4\hfill (1)`

`=(12x^3+8x)+(-6x^2-4)\hfill (2)`

`=(12x^3-6x^2)+(8x-4)\hfill (3)`

To choose correct factor among (2) and (3) of (1).

Consider (2) we get,

`(12x^3+8x)+(-6x^2-4)=4x(3x^2+2)-2(3x^2+2)=(4x-2)(3x^2+2)`

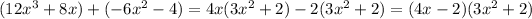
And from (3) we get,

`(12x^3-6x^2)+(8x-4)=3x^2(4x-2)+2(4x-2)=(3x^2+2)(4x-2)`

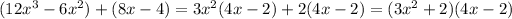
Since (2) and (3) gives same factor and both factors are irreducible and gives values of x directly so we can accept both factors as correct. In case we get different terms of factors in that case we must choose the simplest factor from which we can derive value of x easily.

So both (2) and (3) can correctly grouped the terms to factor.