Answer:
118 children and 251 adults swam at the public pool that day.
Explanation:
Given:
On a certain hot summer's day, 369 people used the public swimming pool. The daily prices are $ 1.25 for children and $ 2.50 for adults. The receipts for admission totaled $ 775.00.
Now, to find the number of children and adults swam at the public pool that day.
Let the number of children be
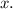
And let the number of adults be
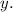
So, total number of people used the swimming pool:
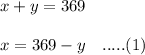
Now, the total price for admission:
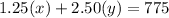
Substituting the value of
 from equation (1) we get:
from equation (1) we get:
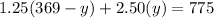
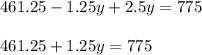
Subtracting both sides by 461.25 we get:
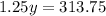
Dividing both sides by 1.25 we get:
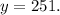
The number of adults = 251.
Substituting the value of
 in equation (1) we get:
in equation (1) we get:
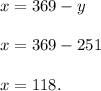
The number of children = 118.
Therefore, 118 children and 251 adults swam at the public pool that day.