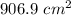Answer:
Explanation:
A do-decagon is a polygon with 12 straight sides and 12 equal angles.
-The general formula for finding area of a do-decagon is given as:
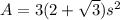
where s is the sides length.
-Given the sides dimension is 9cm, the area is calculated as;
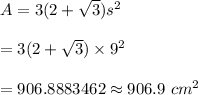
Hence, the do-decagon's area is