Question

Based on the responses a 95 percent confidence interval for the proportion of all students at the school who would respond yes to the question was calculated as (0.584, 0.816) how many students were in the sample selected by the environmental science teacher?

Answer 1

The sample size is 60

Step-by-step explanation:

Using the standard formula for a confidence interval, the interval (0.584 to 0.186) is found by using the formula:

p ±
`z^(*)`
`\sqrt{(p(1-p))/(n) }`

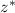
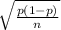
Step 1

Find the value of p

p=
`(0.584+0.816)/(2)`

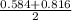
p=0.7

Step 2

Calculate the margin of error

Margin of error= 0.816-0.7

= 0.116

Step 3

Using the above formula, calculate the sample size, i.e value of n

Since its a two tailed test, the critical value of z for 95% confidence level is 1.96,

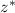`z^(*)`= 1.96

now substitute the values in the above formula:

`1.96\sqrt{(0.7(1-0.7))/(n) } =0.116\\n=(1.96^(2) (0.7)(1-0.7) )/(0.116^(2) )`

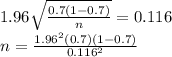
n=59.95 =60

The number of students selected by the teacher were 60

Answer 2

Number of students ; 60

Step-by-step explanation:

Using the formula for p +- z * Sqrt ( pq/n )

Let us first calculate the Margin of Error

= 0.816 –0.7 = 0.116

•z* = 1.96

P = (0.584 + 0.116 ) = 0.7

Q = 1- p = 1 – 0.7 = 0.3

Now inserting the values in the formula; we get

0.116 = 1.96 x sqrt { ( 0.7 x 0.3) / n }

Solving the above equation

N = 60 (rounded off to nearest number)

Hence the number of students that were selected by the environmental teacher in the sample is 60