Question

A specimen of some metal having a rectangular cross section 10.4 mm × 12.8 mm is pulled in tension with a force of 15900 N, which produces only elastic deformation. Given that the elastic modulus of this metal is 79 GPa, calculate the resulting strain.

Answer 1

`\sigma=0.00151`

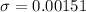
Step-by-step explanation:

We apply Hooke's Law as follows :

`\sigma= E\varepsilon`

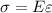
where
`\sigma` is the applied stress

#The applied stress is also equal to :

`\sigma=(F)/(A_o)=(F)/(lw)`

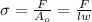
Where
`l\` and
`w` are the cross-sectional dimensions.

=>We equate the two stress equations:

`E\varepsilon=(F)/(lw)\\\\\varepsilon=(F)/(Elw)`

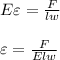
#We substitute our values in the equation as:

`\varepsilon=(15900\ N)/((79* 10^9\ N/m^2)(10.4\ m* 10^(-3)* 12.8\ m* 10^(-3)))}\\\\\\=0.00151`

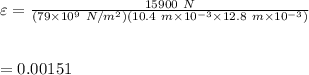
Hence, the resulting strain is 0.00151