Question

A refrigerator should be set at 38*f with an allowance for 2*. 1.) Write an equation to find the maximum temperatures at which the refrigerator should be set. 2.) Solve the equation to find the maximum and minimum temperatures at which the refrigerator should be set.

Answer 1

1) For this case we can use the absolute value and we can write the limit with this expression:

`|T-38| \leq 2`

Where T represent the temperature for the refrigerator in F.

2) If we solve for T we have this:

`-2 \leq T-38 \leq 2`

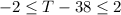
We can add 38 in all the sides of the inequality

`-2+38 \leq T\leq 2+38`

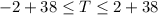
And finally we got:

`36 \leq T \leq 40`

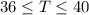
So then the refrigerator can work between 36 F and 40 F for this case.

Explanation:

For this case we know that the refrigerator hould be set at 38 F, and the allowance or the variation is 2F.

Part 1

For this case we can use the absolute value and we can write the limit with this expression:

`|T-38| \leq 2`

Where T represent the temperature for the refrigerator in F.

Part 2

If we solve for T we have this:

`-2 \leq T-38 \leq 2`

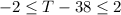
We can add 38 in all the sides of the inequality

`-2+38 \leq T\leq 2+38`

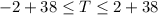
And finally we got:

`36 \leq T \leq 40`

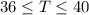
So then the refrigerator can work between 36 F and 40 F for this case.