Question

Two sides and an angle (SSA) of a triangle are given. Determine whether the given measurements produce one triangle, two triangles, or no triangle at all. Solve each triangle that results. Round lengths to the nearest tenth and angle measures to the nearest degree. B = 41°, a = 4, b = 3

Answer 1

Hence, only one triangle is possible.

Explanation:

Let, ABC is a triangle.

Given that,

first side of a ΔABC is 4, second side of a ΔABC is 3 and ∠B is
`41`°.

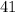Diagram of the ΔABC is shown below.

Now,

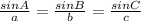`(sinA)/(a)=(sinB)/(b)=(sinC)/(c)` (Law of sines)

`(sinA)/(a)=(sinB)/(b)`

⇒
`(sinA)/(4)= (sin41)/(3)`

⇒
`sinA= (sin41* 4)/(3)` =
`0.87475`

⇒
`sin^(-1) (0.87475)=A`

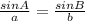
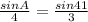
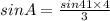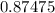
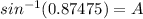
⇒ ∠A = 61°

Now, ∠A + ∠B+ ∠C = 180° (angle sum property)

⇒ 61° + 41° + ∠C = 180°

⇒ ∠C = 78°

`(sinB)/(b)=(sinC)/(c)`

⇒
`(sin41)/(3)=(sin78)/(c)`

⇒
`c=(sin78*3)/(sin41)`

⇒
`c= (0.9782*3)/(0.65606) =4.47`

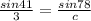
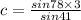
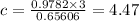
Therefore, ∠A = 61°, ∠B = 41°, ∠C = 78°,
`a=4, b=3, c= 4.47.`

Hence, only one triangle is possible.