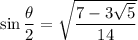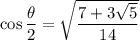Question

Help I can't find the answer

Find the exact values of sin θ/2 and cos θ/2 for sin θ = 2/7 on the interval 0° ≤ θ ≤ 90° .

Answer 1

For angles
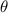`\theta` between 0º and 90º, we know
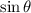`\sin\theta` and
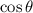`\cos\theta` are both positive.

Then
`\frac\theta2` falls between 0º and 45º, so both
`\sin\frac\theta2` and
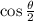`\cos\frac\theta2` are also positive.

Recall the double angle identities,

`\sin^2x=\frac{1-\cos2x}2\implies\sin^2\frac\theta2=\frac{1-\cos\theta}2`

`\cos^2x=\frac{1+\cos2x}2\implies\cos^2\frac\theta2=\frac{1+\cos\theta}2`

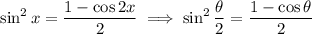
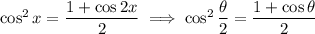
We know sine and cosine should be positive, so taking the square root of both sides gives us

`\sin\frac\theta2=\sqrt{\frac{1-\cos\theta}2}`

`\cos\frac\theta2=\sqrt{\frac{1+\cos\theta}2}`

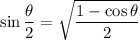
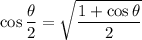
Also recall the Pythagorean identity,

`\cos^2x=1-\sin^2x\implies\cos\theta=√(1-\sin^2\theta)`

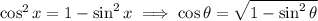
Then

`\cos\theta=√(1-\left(\frac27\right)^2)=\frac{3\sqrt5}7`

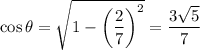
and from here we get

`\sin\frac\theta2=\sqrt{(7-3\sqrt5)/(14)}`

`\cos\frac\theta2=\sqrt{(7+3\sqrt5)/(14)}`