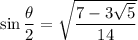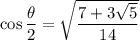For angles
 between 0º and 90º, we know
between 0º and 90º, we know
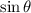 and
and
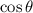 are both positive.
are both positive.
Then
 falls between 0º and 45º, so both
falls between 0º and 45º, so both
 and
and
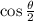 are also positive.
are also positive.
Recall the double angle identities,
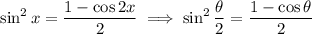
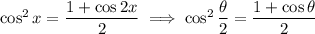
We know sine and cosine should be positive, so taking the square root of both sides gives us
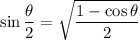
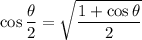
Also recall the Pythagorean identity,
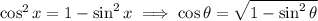
Then
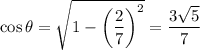
and from here we get