Answer:
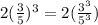 and not
and not
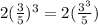
Explanation:
Jim's work evaluating
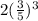 is shown:
is shown:
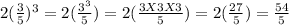
If you look at the Second step, the exponent is taken over only the numerator. It should have been taken over both the numerator and denominator as shown below.
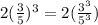
The correct workings therefore is:
