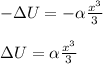Question

In an experiment, one of the forces exerted on a proton is F⃗ =−αx2i^, where α=12N/m2. What is the potential-energy function for F⃗ ? Let U=0 when x=0. Express your answer in terms of α and x.

Answer 1

`\Delta U= \alpha (x^3)/(3) \\`

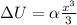
Step-by-step explanation:

given

`F = -\alpha x^2 i`

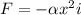
where
`\alpha = 12 N/m^2`

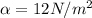
now we know

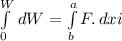`\int\limits^W_0 {} \, dW = \int\limits^a_b {F.} \, dxi` ..................(i)

where dx is infinitesimal distance

`W = \int\limits^a_b {-\alpha x^2} \, dx \\`

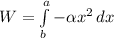
for x = a and b = 0

after integration we get

`W = -\alpha (x^3)/(3)`

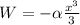
we know work done by conservative force will be equals to negative of potential energy

`W = -\Delta U`

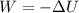
so we get

`-\Delta U= -\alpha (x^3)/(3) \\\\\Delta U= \alpha (x^3)/(3) \\`