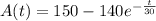Answer:
Therefore, the number of grams of salt in the tank at time t is
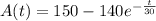
Step-by-step explanation:
Given:
Tank A contain
 lit
lit
Rate
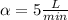
Dissolved salt
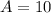 gm
gm
Salt pumped in one minute is
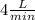
Salt pumped out is
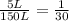 of initial amount added salt.
of initial amount added salt.
To find
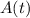
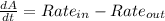
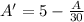
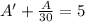
Solving above equation,
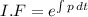
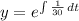
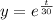
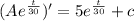
Integrating on both side,
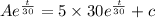
Add
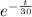 on above equation,
on above equation,
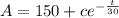
Here given in question,
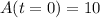
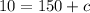
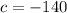
Put value of constant in above equation, and find the number of grams of salt in the tank at time t.
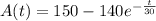
Therefore, the number of grams of salt in the tank at time t is