Question

In right triangle ABC, mC - 90° and AC BC. Which trigonometric ratio is cquivalent to sin b?

Which trigonometric ratio is equivalent to sin A. Which trig ratio is equivalent to cos A? Which trig ratio is

equivalent to Cos B?

Answer 1

Answ

becouse then the thing would be like that

Answer 2

All trigonometric Ratios are
`SinB = (AC)/(AB)` ,
`SinA= (CB)/(AB)` ,
`CosA= (AC)/(AB)`

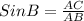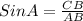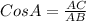
And
`Cos B = (CB)/(AB)`.

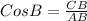Explanation:

Given that,

A right angle triangle ΔABC, ∠C =90°.

Diagram of the given scenario shown below,

In triangle ΔABC :-

`Hypotenuse = AB\\Base = CB\\Perpendicular = AC`

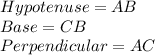
So,
`Sin\theta = (perpendicular)/(hypotenuse)`

`SinB = (AC)/(AB)`

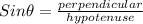
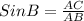
Now, for ∠A the dimensions of trigonometric ratios will be changed.

Here the base for ∠A is AC , perpendicular side is CB and hypotenuse will be same for all ratios.

`SinA= (CB)/(AB)`

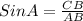
Again,
`Cos\theta= (base)/(hypotenuse)`

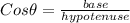
Then,
`CosA= (AC)/(AB)`

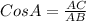
And
`Cos B = (CB)/(AB)`.

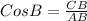Hence,

All trigonometric Ratios are
`SinB = (AC)/(AB)` ,
`SinA= (CB)/(AB)` ,
`CosA= (AC)/(AB)`

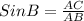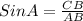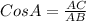
And
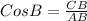`Cos B = (CB)/(AB)`.