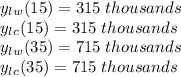Question

The population of two different villages are modeled by the equations shown below. The population (in thousands) is represented by y and the number of years since 1975 is represented by x. What year(s) did the villages have the same population? What was the population of both cities during the year(s) of equal population? Lewiston: y= x^2 - 30x +540; Lockport: y= 20x +15

Answer 1

1990 and 2010

`y_l_w(15)=315\hspace{3}thousands\\y_l_c(15)=315\hspace{3}thousands\\y_l_w(35)=715\hspace{3}thousands\\y_l_c(35)=715\hspace{3}thousands`

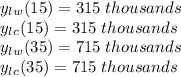
Step-by-step explanation:

Let:

`y_l_w=Population\hspace{3}of\hspace{3}Lewiston\\y_l_c=Population\hspace{3}of\hspace{3}Lockport`

We need to know, in what year(s) the villages had the same population, mathematically this is:

`y_l_w=y_l_c`

So:

`x^2-30x+540=20x+15\\\\Subtract\hspace{3}20x\hspace{3}from\hspace{3}both\hspace{3}sides\\\\x^2-50x+540=15\\\\Subtract\hspace{3}15\hspace{3}from\hspace{3}both\hspace{3}sides\\\\x^2-50x+525=0`

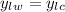
Solving for x:

Factoring

`(x-15)(x-35)=0`

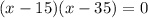
Hence:

`x=15\\\\or\\\\x=35`

Therefore the year(s) which the village had the same population are:

`1975+15=1990\\\\and\\\\1975+35=2010`

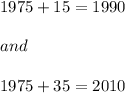
In order to find the population of both cities during the year(s) of equal population, just evalue the equations at x=15 and x=35:

`y_l_w(15)=315\hspace{3}thousands\\y_l_c(15)=315\hspace{3}thousands\\y_l_w(35)=715\hspace{3}thousands\\y_l_c(35)=715\hspace{3}thousands`