Answer:
11.11% probability that Carlo drew a 6
Explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
Possible results:
(Carlo, Eric)
(1,1), (2,1), (3,1), (4,1), (5,1), (6,1), (7,1), (8,1), (9,1),(10,1)
(1,2), (2,2), (3,2), (4,2), (5,2), (6,2), (7,2), (8,2), (9,2),(10,2)
(1,3), (2,3), (3,3), (4,3), (5,3), (6,3), (7,3), (8,3), (9,3),(10,3)
(1,4), (2,4), (3,4), (4,4), (5,4), (6,4), (7,4), (8,4), (9,4),(10,4)
(1,5), (2,5), (3,5), (4,5), (5,5), (6,5), (7,5), (8,5), (9,5),(10,5)
(1,6), (2,6), (3,6), (4,6), (5,6), (6,6), (7,6), (8,6), (9,6),(10,6)
(1,7), (2,7), (3,7), (4,7), (5,7), (6,7), (7,7), (8,7), (9,7),(10,7)
(1,8), (2,8), (3,8), (4,8), (5,8), (6,8), (7,8), (8,8), (9,8),(10,8)
(1,9), (2,9), (3,9), (4,9, (5,9), (6,9), (7,9), (8,9), (9,9),(10,9)
(1,10), (2,10), (3,10), (4,10), (5,10), (6,10), (7,10), (8,10), (9,10),(10,10)
Desired outcomes:
Carlo drawing a six, higer than Eric
(6,1),(6,2),(6,3),(6,4),(6,5)
5 possible outcomes
So D = 5.
Total outcomes:
Given that Carlo's number was higher than Eric's, so only pairs in which Carlo is higher than Eric
(2,1), (3,1), (4,1), (5,1), (6,1), (7,1), (8,1), (9,1),(10,1)
(3,2), (4,2), (5,2), (6,2), (7,2), (8,2), (9,2),(10,2)
(4,3), (5,3), (6,3), (7,3), (8,3), (9,3),(10,3)
(5,4), (6,4), (7,4), (8,4), (9,4),(10,4)
(6,5), (7,5), (8,5), (9,5),(10,5)
(7,6), (8,6), (9,6),(10,6)
(8,7), (9,7),(10,7)
(9,8), (10,8)
(10,9)
45 total outcomes
So T = 45
Probability
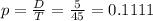
11.11% probability that Carlo drew a 6