Question

D. Based on the residuals, is your regression line a reasonable model for the data? Why or why

not? (2 points)

Answer 1

Based on the residuals, the regression line is a reasonable model for the data. The residuals show a random pattern with no discernible trend, indicating that the model captures the variability in the data, and the errors are not systematically overestimating or underestimating.

Step-by-step explanation:

Residuals are the differences between the observed values and the predicted values from the regression line. To assess the adequacy of the regression model, we examine the pattern of residuals. A reasonable model should have residuals that exhibit a random scatter around zero. If there is a discernible pattern, it suggests that the model is not capturing all the variability in the data.

In this case, after calculating the residuals, if they show no systematic trend, such as all being consistently positive or negative, and they are randomly scattered around zero, it indicates that the regression line is a good fit for the data. This randomness suggests that the model is effectively explaining the variance in the dependent variable, and the residuals do not indicate any systematic bias in the predictions.

In conclusion, the reasonability of the regression model is affirmed by the lack of a discernible pattern in the residuals. The absence of systematic errors in overestimation or underestimation supports the conclusion that the regression line adequately represents the relationship between the variables.

Answer 2

The regression line having minimum residuals, actual values closest to estimated regression line values : depicts the most reasonable data model.

Step-by-step explanation:

Regression is a statistical tool depicting cause effect relationship between independent variable(s) (X) , dependent variable. (Y)

Population Regression Function is the conditional expectation of Yi, based on given Xi.

E (Yi / Xi ) =
`\beta 0 + \beta 1 Xi` ; where Y's value is based on given X values

Sample Regression Function is estimated relationship between Y & X, based on sample study.

y = b0 + b1x1 ; where y is a estimate of Y, b0 & b1 estimates of
`\beta 0 , \beta 1` .

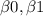In estimating through SRF: there are residuals, i.e differences between actual & estimated values. The most reasonable regression model (regression line) is which minimises the residual values, i.e actual values are closest possible to regression estimated values.

For this matter, classical linear regression model uses 'Ordinary Least Squares' regression, which minimises the residual's squared values.