Question

water in the tank is 2.5 ft. Water enters the tank through a top port of diameter 6 in. at a velocity of 24 ft/s. The water leaves the tank through two exit ports each with a diameter of 6 in. If the scale shows a reading of 585 lbf, calculate the weight of the tank when it is empty

Answer 1

The weight of the tank when it is empty is 501.38 lbf

Step-by-step explanation:

The velocity of outlet is equal to:

`A_(i) v_(i)=2A_(o) v_(o) \\(\pi d_(i)^(2) v_(i) )/(4) =(2\pi d_(o)^(2) v_(o) )/(4)\\v_(o) =(d_(i)^(2) v_(i) )/(2d_(o)^(2) )`

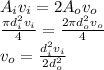
Where

vi = 24 ft/s

di = 6 in = 0.5 ft

do = 6 in = 0.5 ft

`v_(o) =(0.5^(2)*24 )/(2*0.5^(2) ) =12ft/s`

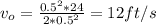
The total weight of the water excluding the tank weight is equal to:

`W=pv_(i)^(2) +pghA_(tank) -pv_(o)^(2) =p(v_(i)+gh((\pi d_(tank)^(2) )/(4) -v_(o)^(2) ))`

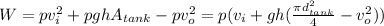
p = 62.43 lb/ft³

dtank = 20 in = 1.67 ft

Replacing:

`W=62.43(24^(2) +(32.17*2.5*((\pi 1.67^(2) )/(4) )-12^(2) )=37929.5 lb=83.62lbf`

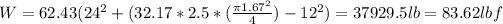
The weight of the tank is:

Wtank = 585 - 83.62 = 501.38 lbf