Answer:
height = 5.33 m (nearest hundredth)
area of wall = 41.66 m² (nearest hundredth)
Explanation:
To find the height of A above the ground, find the height of the triangle and add it to the height of the rectangle.
The dashes on the sides of the triangle mean they are equal in length. Therefore, this triangle is an isosceles. If we draw a line down the center of the triangle to create 2 right triangles, their top angles will be 65° (half of 130°) and they will each have a base length of 5 m (see attached diagram).
To find the height, use the tan trig ratio:
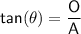
where:
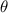 = angle
= angle- O = side opposite the angle
- A = side adjacent to the angle
Given:
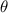 = 65°
= 65°- O = 5 m
- A = h

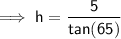
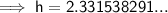
Therefore, the height of A above the ground:
⇒ height = 3 + 2.331538191 = 5.33 m (nearest hundredth)
----------------------------------------------------------------------------------------
To find the area of the wall, sum the area of the rectangle and the area of the triangle.
Area of rectangle = width x height
= 3 x 10
= 30 m²
Area of triangle = 1/2 x base x height
= 1/2 x 10 x 2.331538191
= 11.65769145 m²
Total area of wall = 30 + 11.65769145 = 41.66 m² (nearest hundredth)