Answer:
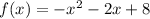
y-intercept is when x = 0:

So the y-intercept is (0, 8)
x-intercepts are when f(x) = 0:
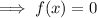
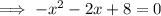
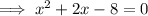
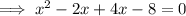
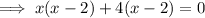
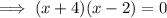
Therefore:
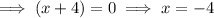
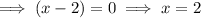
So the x-intercepts are (-4, 0) and (2, 0)
The vertex is the turning point of the parabola. The x-value of the vertex is the x-value between the 2 zeros (x-intercepts).
Therefore, the x-value of the vertex is
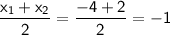
Substituting x = -1 into the function:
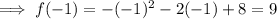
So the vertex is (-1, 9)
The domain is the input values, so x = all real numbers.
The range is the output values, so the range is
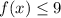
Therefore, (-4, 0), (-1, 9), (0, 8) and (2, 0) are solutions of the function, HOWEVER they are not ALL the solutions.
All solutions of the function are:
 for all real numbers of x
for all real numbers of x