Question

Which is a factor of x2 – 9x + 14?
x – 9
x – 2
x + 5
x + 7

Answer 1

x-2

Explanation:

Let's factor x2−9x+14

x2−9x+14

The middle number is -9 and the last number is 14.

Factoring means we want something like

(x+_)(x+_)

Which numbers go in the blanks?

We need two numbers that...

Add together to get -9

Multiply together to get 14

Can you think of the two numbers?

Try -2 and -7:

-2+-7 = -9

-2*-7 = 14

Fill in the blanks in

(x+_)(x+_)

with -2 and -7 to get...

(x-2)(x-7)

Answer:

(x−2)(x−7)

Answer 2

The binomial: (x-2) (second option of the list) is a factor of the given trinomial

Explanation:

You are looking for two binomial factors of the form; (x+a) and (x+b), with values "a" and "b" such that:

Their product "a times b" results in: "+14" (the numerical term in the initial trinomial
`x^2-9x+14`,

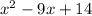and their combining "a+b" results in "-9" (the coefficient in the middle term of the trinomial)

Such number "a" and "b" are: "-2" and "-7".

We can see by multiplying the binomials formed with these numbers:

(x-2) and (x-7) that their product indeed renders the original trinomial:

`(x-2) (x-7)= x^2-7x-2x+14=x^2-9x+14`

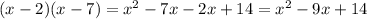
therefore, the binomials (x-2) and (x-7) are factors of the given trinomial.

The only one shown among the four possible options is then: (x-2)