The ratio of their area is 81 : 1.
Explanation:
Given,
The perimeter of two equilateral triangles is 9:1
To find the ratio of their areas.
Formula
If each side of a equilateral triangle is a then perimeter = 3a and area =
 a²
a²
Now,
Perimeter of the 1st triangle is 9x
So, each side will be 3x
Again,
Perimeter of the 2nd triangle is x
So, each side will be
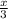
Now,
Area of the 1st triangle =
 (3x)²
(3x)²
Area of the 2nd triangle =
 (
(
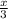 )²
)²
Hence,
The ratio of their area =
 (3x)² :
(3x)² :
= 9x² :

= 81 : 1
Thus the obtained ration of the triangle is 81:1