Answer:
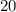 .
.
Explanation:
In any triangle, the sum of the lengths of any two sides should be strictly greater than the length of the third side. For example, if the length of the three sides are
 ,
,
 , and
, and
 :
:
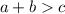 ,
,
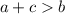 , and
, and
 .
.
In this question, the length of the sides are
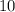 ,
,
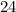 , and
, and
 . The length of these sides should satisfty the following inequalities:
. The length of these sides should satisfty the following inequalities:
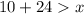 ,
,
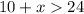 , and
, and
 .
.
Since
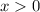 , the inequality
, the inequality
 is guarenteed to be satisfied.
is guarenteed to be satisfied.
Simplify
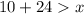 to obtain the inequality
to obtain the inequality
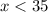 .
.
Similarly, simplify
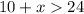 to obtain the inequality
to obtain the inequality
 .
.
Since
 needs to be a whole number, the greatest
needs to be a whole number, the greatest
 that satisfies
that satisfies
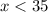 would be
would be
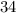 . Similarly, the least
. Similarly, the least
 that satisfies
that satisfies
 would be
would be
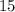 . Thus,
. Thus,
 could be any whole number between
could be any whole number between
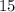 and
and
 (inclusive.)
(inclusive.)
There are a total of
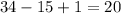 distinct whole numbers between
distinct whole numbers between
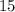 and
and
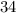 (inclusive.) Thus, the number of possible whole number values for
(inclusive.) Thus, the number of possible whole number values for
 would be
would be
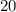 .
.