Question

16. The area of a parallelogram is 120. If the base is reduced to one-half its original length, and its height is quadrupled, what is the new area?

(20 pts)

30

60

120

240

Answer 1

Correct option is D) 240 .

Explanation:

Here we have , The area of a parallelogram is 120. If the base is reduced to one-half its original length, and its height is quadrupled, We need to find new area . Let's find out:

We know that area of parallelogram is given by :

⇒
`Area = B(h)`

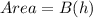
According to question , New dimensions are

`B = (1)/(2) B\\h = 4h`

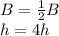
So ,

⇒
`Area = B(h)`

⇒
`Area = ((1)/(2) B)(4h)`

⇒
`Area = 2B(h) = 2(120)`

⇒
`Area = 240`

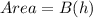
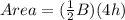
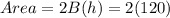
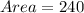
Therefore , Correct option is D) 240 .