The Length of the rectangle is 14
 m and width 9
m and width 9
 m.
m.
Explanation:
Given,
Perimeter of the rectangle = 48 m
The width of the rectangle is 2 more than half the length.
To find the length and width of the rectangle.
Formula
Perimeter of the rectangle of length l and width b is = 2(l+b)
Let,
Length = l
Width =
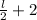 [ given]
[ given]
Now,
According to the problem
2(l+
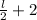 ) = 48
) = 48
or,
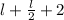 = 24
= 24
or,
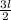 = 24-2
= 24-2
or,
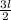 = 22
= 22
or, l =
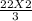 =
=
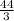 = 14
= 14

And width =
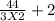 =
=
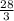 = 9
= 9

Hence,
Length = 14
 m and width = 9
m and width = 9
 m
m