Answer:
(x+5)(x+7)
Explanation:
We need to find two binomials of the form (x+a) and (x+b) such that their product gives
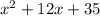
So, notice that the values for "a" and for "b" in the binomials to factor should verify that :
1) a * b = 35
and 2) a+b = 12
Since the product (x+a) times (x+b) =
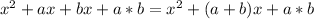
The pair of values 7 and 5 satisfy such conditions.
Therefore (x+5) (x+7) =
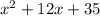
and then (x+5) and (x+7) are binomial factors of the original trinomial.