Answer:
0.0097 mol·L⁻¹
Step-by-step explanation:
The balanced equation is
2NOCl ⇌ 2NO₂ + Cl₂
Data:
Your value of Kc is incorrect. It should be
Kc =1.6 × 10⁻⁵
[NOCl] = 0.50 mol·L⁻¹
[NO] = 0.00 mol·L⁻¹
[Cl₂] = 0.00 mol·L⁻¹
Calculations:
1. Set up an ICE table.
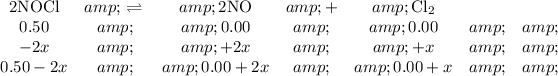
2. Calculate the equilibrium concentrations
![K_{\text{c}} = \frac{\text{[NO]$^(2)$[Cl$_(2)$]}}{\text{[NOCl]}^(2)} = ((2x)^(2)(x))/((0.50 - 2x)^(2)) = 1.6 * 10^(-5)\\\\4x^(3) = 1.6 * 10^(-5)(0.50 - 2x)^(2)\\x^(3) = 4.0 * 10^(-6)(0.50 - 2x)^(2)](https://img.qammunity.org/2021/formulas/chemistry/middle-school/lgrs0wzznwrmruai5pg9idit5h7ck6l8i5.png)
This is a cubic equation. Some calculators can solve cubic equations, but we can solve it by the method of successive approximations.
We will make changes to the right-hand side until the calculated value of x no longer changes,
(a) 1st approximation
Assume that 2x is negligible compared to 0.50. Then
![x = \sqrt [3] {4.0 * 10^(-6)(0.50)^(2)} = 0.010](https://img.qammunity.org/2021/formulas/chemistry/middle-school/ykogi68q0zk91u03zaxmb673pzut2r24kz.png)
(b) 2nd approximation
Assume that x= 0.010. Then
![x = \sqrt [3] {4.0 * 10^(-6)(0.50 - 2* 0.010)^(2)} = 0.0097](https://img.qammunity.org/2021/formulas/chemistry/middle-school/391r3vnmhqcevc4ucqec5giq1ytzth9efz.png)
(b) 3rd approximation
Assume that x= 0.0097. Then
![x = \sqrt [3] {4.0 * 10^(-6)(0.50 - 2* 0.0097)^(2)} = 0.0097](https://img.qammunity.org/2021/formulas/chemistry/middle-school/td9fx8uwc804v7bbb8fwpvpmywfrygdral.png)
No change, so x = 0.0097.
[Cl₂] = x mol·L⁻¹ = 0.0097 mol·L⁻¹
Check:
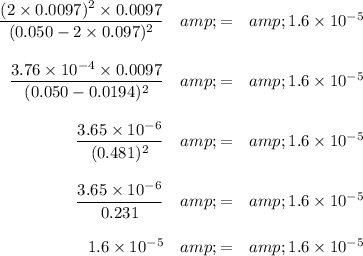
It checks.