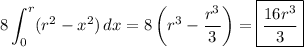I assume the base of S is the disk centered at the origin, or x² + y² ≤ r². Solving for y gives two solutions corresponding to the upper and lower halves of the circular boundary,
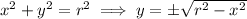
and the vertical distance between them - i.e. the side length of each cross section - is
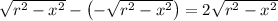
Then the volume of each square cross section 4 (r² - x²) ∆x, and the volume of S is
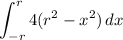
By symmetry, this is the same as

which gives a volume of