Answer:
the radius of the circle is changing
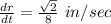 at that time.
at that time.
Explanation:
Given:
Area of Circle
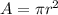
Radius
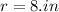
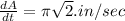
We need to find the radius of the circle changing at this time
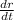 .
.
Solution:
To find the rate at which the radius of the circle is changing with respect to time we will apply derivative on Area of the circle.
Now we know that;
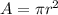
Applying derivative we get;
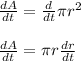
Now substituting the given value we get;
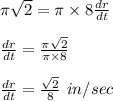
Hence the radius of the circle is changing
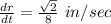 at that time.
at that time.