Question

A dumbbell-shaped object is composed by two equal masses, m, connected by a rod of negligible mass and length r. If I1 is the moment of inertia of this object with respect to an axis passing through the center of the rod and perpendicular to it and I2 is the moment of inertia with respect to an axis passing through one of the masses we can say that

Answer 1

Relation between two moment of inertia is

`I_2 = 2I_1`

Step-by-step explanation:

Here we know that moment of inertia of the object from an axis passing through mid point and perpendicular to the plane is given as

`I_1 = m((r)/(2))^2 + m((r)/(2))^2`

`I_1 = (mr^2)/(2)`

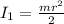
now moment of inertia about an axis passing through one of the mass is given as

`I_2 = mr^2 + 0`

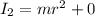
now we have

`I_2 = 2I_1`