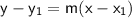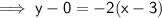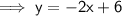Question

I dont really know what to do here, ive done a which is -2 but dont know how to do b. It is not 1/2x -1.5

Answer 1

a) -2

b) y = -2x + 6

Explanation:

Question (a)

Point A = (-1, -2)

Point B = (7, 2)

`\sf gradient\:of\:AB=(change\:in\:y)/(change\:in\:x)=(2-(-2))/(7-(-1))=(4)/(8)=\frac12`

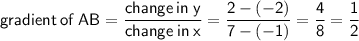
If lines are perpendicular to each other, the product of their gradients will be -1.

Let g be the gradient of the perpendicular line:

`\implies \sf \frac12 * g=-1`

`\implies \sf g=-1 / \frac12=-2`

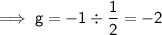
Therefore, the gradient of the line perpendicular to AB is -2

---------------------------------------------------------------------------------------------

Question (b)

`\sf midpoint\:of\:line = \left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`\sf let\:point\:A=(x_1,y_1)=(-1,-2)`

`\sf let\:point\:B=(x_2,y_2)=(7,2)`

`\sf \implies midpoint\:of\:line\:AB = \left((-1+7)/(2),(-2+2)/(2)\right)=(3,0)`

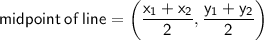
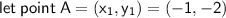
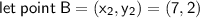
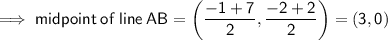
We now know the gradient and a point on the perpendicular line.

So we can use the point-slope form of a linear equation:

`\sf y-y_1=m(x-x_1)`

`\implies \sf y-0=-2(x-3)`

`\implies \sf y=-2x+6`