Answer:
a)
 , b)
, b)
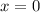 ,
,
 , c)
, c)
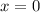 , d)
, d)

Explanation:
a) Let derive the function:
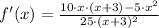
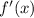 is undefined when denominator equates to zero. The critical point is:
is undefined when denominator equates to zero. The critical point is:

b)
 when numerator equates to zero. That is:
when numerator equates to zero. That is:
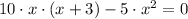
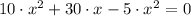
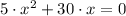
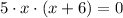
This equation shows two critical points:
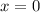 ,
,

c) The critical points found in point b) and the existence of a discontinuity in point a) lead to the conclusion of the existence local minima and maxima. By plotting the function, it is evident that
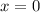 corresponds to a local maximum. (See Attachment)
corresponds to a local maximum. (See Attachment)
d) By plotting the function, it is evident that
 corresponds to a local minimum. (See Attachment)
corresponds to a local minimum. (See Attachment)