Question

An arcade booth at a county fair has a person pick a coin from two possible coins available and then toss it. If the coin chosen lands on heads, the person gets a prize. One coin is a fair coin and one coin is a biased coin (unfair) with only a 32% chance of getting ahead. Assuming the equally likely probability of picking either coin, what is the probability that the fair coin is the one chosen, given that the chosen coin lands on heads?

a. 0.8300
b. 0.6024
c. 0.0149
d. 0.4150
e. 0.4310

Answer 1

b. 0.6024

Explanation:

Conditional Probability

Suppose two events A and B are not independent, i.e. they can occur simultaneously. It means there is a space where the intersection of A and B is not empty:

`P(A\cap B) \\eq 0`

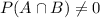
If we already know event B has occurred, we can compute the probability that event A has also occurred with the conditional probability formula

`\displaystyle P(A|B)=(P(A\cap B))/(P(B))`

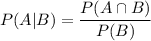
Now analyze the situation presented in the question. Let's call F to the fair coin with 50%-50% probability to get heads-tails, and U to the unfair coin with 32%-68% to get heads-tails respectively.

Since the probability to pick either coin is one half each, we have

`P(U)=P(F)=50\%=0.5`

If we had picked the fair coin, the probability of getting heads is 0.5 also, so

`P(F\cap H)=0.5\cdot 0.5=0.25`

If we had picked the unfair coin, the probability of getting heads is 0.32, so

`P(U\cap H)=0.32\cdot 0.5=0.16`

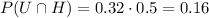
Being A the event of choosing the fair coin, and B the event of getting heads, then

`P(B)=P(F\cap H)+P(U\cap H)=0.25+0.16=0.41`

`P(A\cap B)=P(F\cap H)=0.25`

`\displaystyle P(A|B)=(0.25)/(0.41)=0.61`

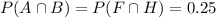
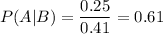
The closest answer is

b. 0.6024