To find out which values of x makes the inequality true, you can either plug in the values into the inequality or solve the inequality to determine what values "x" can be:
Solve the inequality:
To solve the inequality, you need to isolate/get the variable "x" by itself in the inequality
-3(x + 1) > 15 Divide -3 on both sides
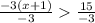When you multiply/divide by a negative number in an inequality, you have to flip the sign (</>)
x + 1 < -5 Subtract 1 on both sides to get "x" by itself
x < -6 [x is any value less than -6]
This means that x can't be -6 or a number above -6, so the values of x that make the inequality true = -9, -8, and -7
Plug the values in:
x = -9
-3(x + 1) > 15 Substitute/plug in -9 into "x" since x = -9
-3(-9 + 1) > 15
-3(-8) > 15 [two negative signs cancel each other out and become positive]
24 > 15 This is true because 24 is greater than 15
x = -8
-3(x + 1) > 15 Plug in -8 into "x"
21 > 15 This is true because 21 is greater than 15
x = -7
-3(x + 1) > 15 Plug in -7 into "x"
18 > 15 This is true because 18 is greater than 15
x = -6
15 > 15 This is false because 15 is not greater than itself
x = -5
12 > 15 This is false because 12 is not greater than 15
x = -4
9 > 15 This is false because 9 is not greater than 15