Given:
The given equation is
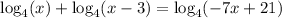
We need to determine the extraneous solution of the equation.
Solving the equation:
To determine the extraneous solution, we shall first solve the given equation.
Applying the log rule
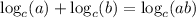 , we get;
, we get;
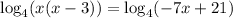
Again applying the log rule, if
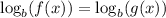 then
then
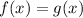
Thus, we have;
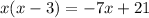
Simplifying the equation, we get;
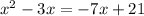
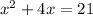
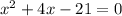
Factoring the equation, we get;
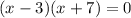
Thus, the solutions are
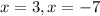
Extraneous solutions:
The extraneous solutions are the solutions that does not work in the original equation.
Now, to determine the extraneous solution, let us substitute x = 3 and x = -7 in the original equation.
Thus, we get;
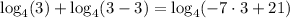
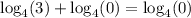
Since, we know that
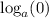 is undefined.
is undefined.
Thus, we get;
Undefined = Undefined
This is false.
Thus, the solution x = 3 does not work in the original equation.
Hence, x = 3 is an extraneous solution.
Similarly, substituting x = -7, in the original equation. Thus, we get;
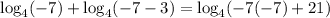
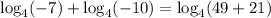
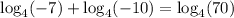
Simplifying, we get;
Undefined =
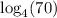
Undefined = 3.06
This is false.
Thus, the solution x = -7 does not work in the original solution.
Hence, x = -7 is an extraneous solution.
Therefore, the extraneous solutions are x = 3 and x = -7