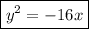Question

Find the standard form of the equation of the parabola with a focus at (-4, 0) and a directrix at x = 4.

Answer 1

`y^2=-16x`

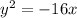
Explanation:

Equation of the Parabola

The standard form of the parabola with the axis of symmetry parallel to the y-axis, vertex at (h.k) and directrix y=k-p is

`(x-h)^2=4p(y-k)`

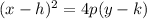
If the parabola has its axis of symmetry parallel to the x-axis, vertex at (h.k) and directrix x=h-p is

`(y-k)^2=4p(x-h)`

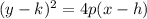
The focus of this form of the parabola is located at (h+p,k)

The parabola described in the question belongs to the second form since the directrix is at x=4. We also know that the focus is at (-4,0). We can find the values of h and p by equating

`h+p=-4`

`h-p=4`

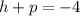
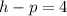
Adding up both equations

`2h=0`

`h=0`

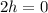
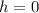
then

`p=-4`

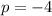
The vertex is (h,k)=(0,0)

We can now write the equation of the parabola as

`(y-0)^2=4\cdot -4(x-0)`

Simplifying

`\boxed{y^2=-16x}`