Answer:
 , where
, where
 is the density of the liquid, and
is the density of the liquid, and
 is the value of gravitational acceleration.
is the value of gravitational acceleration.
Explanation:
Let
 be the density of a liquid. Let
be the density of a liquid. Let
 represent the gravitational acceleration (near the surface of the earth,
represent the gravitational acceleration (near the surface of the earth,
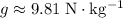 .)
.)
The pressure
 at a depth of
at a depth of
 under the surface of this liquid would be
under the surface of this liquid would be
 .
.
Here's how to deduce this equation from the definition of pressure.
Pressure is the amount of force on a surface per unit area. For example, if a force of
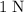 is applied over a surface with an area of
is applied over a surface with an area of
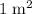 , then the pressure on that surface would be
, then the pressure on that surface would be
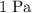 (one Pascal.)
(one Pascal.)
Consider a flat, square object that is horizontally submerged under some liquid at a depth of
 . Assume that
. Assume that
 is the area of that square. The volume of the liquid that sits on top of this square would be
is the area of that square. The volume of the liquid that sits on top of this square would be
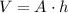 . If the density of that liquid is
. If the density of that liquid is
 , then the mass of that much liquid would be
, then the mass of that much liquid would be
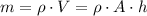 .
.
The weight of that much liquid would be
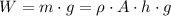 . The liquid on top of that object would exert a force of that size on the object. Since that force is exerted over an area of
. The liquid on top of that object would exert a force of that size on the object. Since that force is exerted over an area of
 , the pressure on the object would be
, the pressure on the object would be
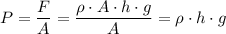 .
.
In this question,
 . As a side note, if
. As a side note, if
 and
and
 are also in standard units (
are also in standard units (
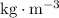 for
for
 and
and
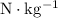 for
for
 ), then
), then
 would be in Pascals (
would be in Pascals (
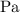 , where
, where
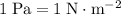 .)
.)