Answer:
a)
 μΩ
μΩ
b)

c)
 Ω
Ω
here * stand for multiplication
Step-by-step explanation:
length of cylinder = 1.5 m
radius of cylinder = 1.1 cm
resistivity depends on the distance x from the left
 ............(i)
............(i)
using equation
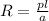
let dR is the resistance of thickness dx
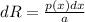
where p(x) is resistivity l is length
a is area
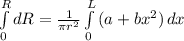 .........................(2)
.........................(2)
after integration
![R = ([aL+(bL^3)/(3)] )/(\pi r^2)](https://img.qammunity.org/2021/formulas/physics/high-school/2ien0s6ug0hco6hh70q405v05obikubugk.png) ...............(3)
...............(3)
it is given
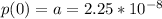 Ωm
Ωm
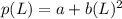 =
=
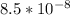 Ωm
Ωm
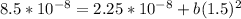
(here * stand for multiplication )
on solving we get
 Ωm
Ωm
put each value of a and b and r value in equation 3rd we get
![R = ([aL+(bL^3)/(3)] )/(\pi r^2)](https://img.qammunity.org/2021/formulas/physics/high-school/2ien0s6ug0hco6hh70q405v05obikubugk.png)
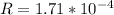 Ω
Ω
 μΩ
μΩ
FOR (b)
for mid point x = L/2
E = p(x)L
for x = L/2
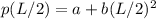
for given current I = 1.75 A
so electric field
![E = ([a+b(L/2)^2]I )/(\pi r^2)](https://img.qammunity.org/2021/formulas/physics/high-school/h5c5hd6zpk6dao0loinfj913yencft3qp8.png)
by substitute the values
we get;

(here * stand for multiplication )
c ).
75 cm means length will be half
that is x = L/2
integrate the second equation with upper limit L/2
Let resistance is
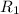
so after integration we get
![R_(1) = ([a(L/2) +(b/3)(L^3/8)])/(\pi r^2)](https://img.qammunity.org/2021/formulas/physics/high-school/nmujpq003eem6odwvv6c6ouj4y5pgsgre0.png)
substitute the value of a , b and L we get
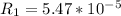 Ω
Ω
for second half resistance

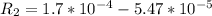
 Ω
Ω
(here * stand for multiplication )