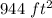Question

The ratio of the areas of two similar polygons is 16 : 81.

a) If the perimeter of the smaller polygon is 424 ft, what is the perimeter of the larger polygon?

b) If the area of the larger polygon is 4779 ft2, what is the area of the smaller polygon?

Answer 1

`a. \ \ \ P_l=954 \ ft\\\\b.\ A_s=944 \ ft^2`

Explanation:

a. Given that the area's are in the ratios 16:81.

-Area is two-dimensional while perimeter is one-dimensional

=>The perimeter's of the two polygons will vary in a ratio equal to the square root of their area's ratio:

`P_s:P_b=√(A_s):√(A_b)\\\\=√(16):√(81)\\\\=4:9`

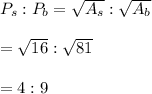
We use the perimeter ratio to find the perimeter of the larger polygon:

`(P_s)/(P_l)=(4)/(9)=(424)/(P_l)\\\\P_l=(424* 9)/4\\\\=954\ ft`

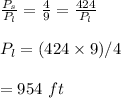
Hence, the perimeter of the larger polygon is 954 ft

b -Given the area of the larger polygon is 4779 ft2, the smaller polygon can be determined using the area ratio 16:81

`(A_s)/(A_l)=(A_s)/(4779)=(16)/(81)\\\\A_s=(4779* 16)/(81)\\\\=944`

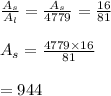
Hence, area of the smaller polygon is
`944 \ ft^2`