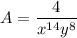Answer:
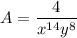
Explanation:
Properties of Powers
The algebraic expression called power has the form x^y where x is called the base and y is called the exponent.
Powers have some properties, some of which we'll recall below

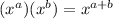



We'll use those properties to simplify the expression
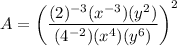
Taking the power 2 of every term
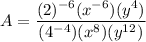
Moving the terms with negative exponent to its opposite side
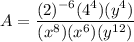
Operating the explicit same bases
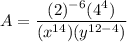
Since
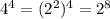
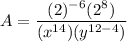
Operating the remaining like bases subtractions
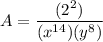
Finally