Question

one leg of a triangle is 28 inches longer than the smaller leg, and the hypotenuse is 32 inches longer than the smaller leg. Find the lengths of the sides of the triangle.

Answer 1

sides of triangle is 20 inches , ( 20 +28) = 48 inches , ( 20 +32 ) = 52 inches !

Step-by-step explanation:

Here we have , one leg of a triangle is 28 inches longer than the smaller leg, and the hypotenuse is 32 inches longer than the smaller leg. We need to Find the lengths of the sides of the triangle. Let's find out:

Let the smaller side be x ,So

one leg of a triangle is 28 inches longer than the smaller leg

We have the following length of side as :

⇒
`x+28`

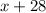
the hypotenuse is 32 inches longer than the smaller leg

We have the following length of hypotenuse as :

⇒
`x+32`

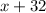
Now , By Pythagoras Theorem :

⇒
`Hypotenuse^2 = Perpendicular^2+Base^2`

⇒
`(x+32)^2 = (x)^2+(x+28)^2`

⇒
`x^2+1024+64x = x^2+x^2+784+56x`

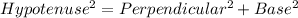
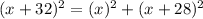
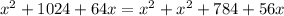
Simplifying we get :

⇒
`x^2-240-8x=0`

⇒
`x^2-8x=240`

⇒
`x^2-8x+16=240+16`

⇒
`(x-4)^2=256`

⇒
`(x-4)^2=16^2`

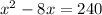
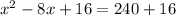
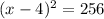
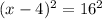
Taking square root both sides we get :

⇒
`x-4= \pm 16`

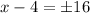
Since , side can't be negative hence :

⇒
`x-4= 16`

⇒
`x=20in`

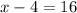
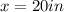
Therefore , sides of triangle is 20 inches , ( 20 +28) = 48 inches , ( 20 +32 ) = 52 inches !

Answer 2

The sides of the triangle are 20 in, 48 in and 52 in

Step-by-step explanation:

Given:

Let x be the length of smaller leg

Hypotenuse, H = x + 32

Height, h = x + 28

Length of the sides of a triangle = ?

If the triangle is a right angle triangle then we use pythagoras theorm to solve the question.

So,

(Hypotenuse)² = (height)² + (Base)²

(x + 32)² = (x + 28)² + (x)²

x² + 1024 + 64x = x² + 784 + 56x + x²

240 + 8x - x² = 0

x² - 8x - 240 = 0

Solving the quadratic equation:

x² + 12x - 20x - 240 = 0

x(x+12) - 20(x+12) = 0

(x-20) (x+12) = 0

(x-20) = 0

x = 20 in

Hypotenuse, H = x + 32

H = 20 + 32 in

H = 52 in

Height, h = x + 28

h = 20 + 28 in

h = 48 in

Therefore, the sides of the triangle are 20 in, 48 in and 52 in