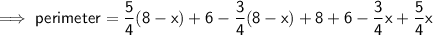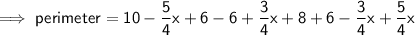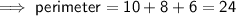Question

ABC is a right triangle at B such that

AB = 8 cm and AC = 10 cm.
1° Calculate BC
2º Consider a point M of the segment [AB]
The line passing through M and parallel to the
line (AC) cuts the line (BC) in N.
Supposing that AM = x, calculate MB and BN in
5
terms of x. then verify that MN (8 - x).
4
3° Let D be the fourth vertex of rectangle
ABCD.
The parallel to (BD) passing through M.cuts the
line (AD) at P
Calculate AP and MP in terms of x
4° Prove that the perimeter of the polygon
MNCDP is independent from x

Answer 1

Question 1

Pythagoras' Theorem: a² + b² = c²

(where a and b are the legs, and c is the hypotenuse, or a right triangle)

Given:

• a = BC
• b = AB = 8cm
• c = AC = 10 cm

⇒ BC² + 8² = 10²

⇒ BC² = 36

⇒ BC = 6 cm

Question 2

Given:

• AB = 8 cm
• AM = x

⇒ MB = AB - AM = 8 - x

As ΔABC ~ ΔMBN

⇒ AB : AC = MB : MN

⇒ 8 : 10 = (8 - x) : MN

`\sf \implies (8)/(10)=((8-x))/(MN)`

`\sf \implies \frac45=((8-x))/(MN)`

`\sf \implies MN=\frac54(8-x)`

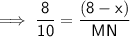
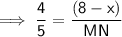
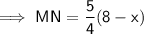
Question 3

D = (6, 8)

As ΔBAD ~ ΔMAP

⇒ AB : AD : BD = AM : AP : MP

⇒ 8 : 6 : 10 = x : AP : MP

`\sf \implies (8)/(6)=(x)/(AP)`

`\sf \implies AP=\frac34x`

`\sf \implies (8)/(10)=(x)/(MP)`

`\sf \implies MP=\frac54x`

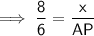
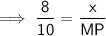
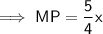
Question 4

Perimeter of MNCDP = MN + NC + CD + PD + MP

As ΔABC ~ ΔMBN

⇒ AB : BC : AC = MB : BN : MN

⇒ 8 : 6 = (8 - x) : BN

`\sf \implies \frac86=((8-x))/(BN)`

`\sf \implies BN=\frac34(8-x)`

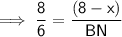
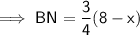
NC = BC - BN

`\sf \implies NC=6-\frac34(8-x)`

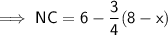
PD = 6 - AP

`\sf \implies PD=6-\frac34x`

Perimeter of MNCDP = MN + NC + CD + PD + MP

`\sf \implies perimeter=\frac54(8-x)+6-\frac34(8-x)+8+6-\frac34x+\frac54x`

`\sf \implies perimeter=10-\frac54x+6-6+\frac34x+8+6-\frac34x+\frac54x`

`\sf \implies perimeter=10+8+6=24`