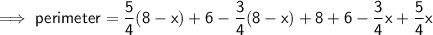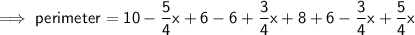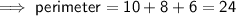Answer:
Question 1
Pythagoras' Theorem: a² + b² = c²
(where a and b are the legs, and c is the hypotenuse, or a right triangle)
Given:
- a = BC
- b = AB = 8cm
- c = AC = 10 cm
⇒ BC² + 8² = 10²
⇒ BC² = 36
⇒ BC = 6 cm
Question 2
Given:
⇒ MB = AB - AM = 8 - x
As ΔABC ~ ΔMBN
⇒ AB : AC = MB : MN
⇒ 8 : 10 = (8 - x) : MN
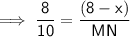
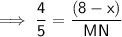
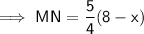
Question 3
D = (6, 8)
As ΔBAD ~ ΔMAP
⇒ AB : AD : BD = AM : AP : MP
⇒ 8 : 6 : 10 = x : AP : MP
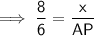
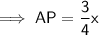
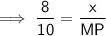
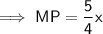
Question 4
Perimeter of MNCDP = MN + NC + CD + PD + MP
As ΔABC ~ ΔMBN
⇒ AB : BC : AC = MB : BN : MN
⇒ 8 : 6 = (8 - x) : BN
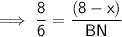
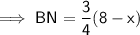
NC = BC - BN
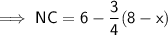
PD = 6 - AP
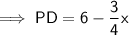
Perimeter of MNCDP = MN + NC + CD + PD + MP